Quaternions

Rotation Representations: Quaternions

To overcome the singularity issue of Gimbal Lock found in Euler angles, we can use a different mathematical tool called quaternions.

What is a Quaternion?

At its core, a quaternion is a four-dimensional number. It's an extension of complex numbers, and it's written as:

q = w + x i + y j + z k

where $w, x, y, z$ are real numbers, and $i, j, k$ are the quaternion units.

For 3D rotations, it's more practical to think of a quaternion as having two parts: a scalar part ( $w$ ) and a 3D vector part ( $\vec{v}$ ).

q = [w, \vec{v}] where \vec{v} = [x, y, z]

To represent a rotation, we must use a unit quaternion, which means its magnitude is 1: $\sqrt{w^{2} + x^{2} + y^{2} + z^{2}} = 1$ .

Quaternions and the Axis-Angle Representation

The real power of quaternions is how elegantly they encode a rotation. A quaternion directly represents a rotation of angle $θ$ around a single, arbitrary unit vector axis $\hat{u} = [u_{x}, u_{y}, u_{z}]$ .

This problem is really hard using Euler, Rotation-About-An-Axis.

The conversion is given by:

w = \cos (\frac{θ}{2})

x = u_{x} \sin (\frac{θ}{2})

y = u_{y} \sin (\frac{θ}{2})

z = u_{z} \sin (\frac{θ}{2})

This axis-angle formulation is what allows quaternions to represent any 3D orientation smoothly and without singularities.

Properties

Addition and subtraction: Quaternions can be added and subtracted component-wise, similar to vectors.

q_{a} \pm q_{b} = [s_{a} \pm s_{b}, v_{a} \pm v_{b}]

Multiplication: Quaternion multiplication is not commutative (i.e., $q_{a} q_{b} \neq q_{b} q_{a}$ ). The multiplication of two quaternions combines their rotations.

q_{a} q_{b} = [s_{a} s_{b} - v_{a}^{T} v_{b}, s_{a} v_{b} + s_{b} v_{a} + v_{a} \times v_{b}]

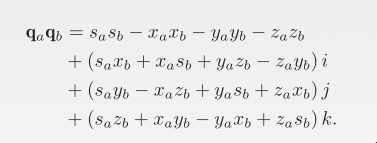
Conjugate: The conjugate of a quaternion $q = [w, \vec{v}]$ is given by $q^{*} = [w, - \vec{v}]$ . This operation is useful for reversing rotations.

q^{*} q = q q^{*} = [s^{2} + v^{T} v, 0]^{T}

Norm: The norm (or magnitude) of a quaternion is given by $| | q | | = \sqrt{w^{2} + x^{2} + y^{2} + z^{2}}$ . For unit quaternions, this norm is 1.
Inverse: The inverse of a unit quaternion $q$ is simply its conjugate, i.e., $q^{- 1} = q^{*}$ . Otherwise it's given by:

q^{- 1} = \frac{q^{*}}{| | q | |^{2}}

Rotation of a vector: To rotate a vector $\vec{p}$ in 3D space using a quaternion $q$ , we first represent the vector as a pure quaternion $p = [0, \vec{p}]$ . The rotated vector $p^{'}$ is obtained by:

p^{'} = q p q^{- 1}

Pasted image 20250929230627.png

Conversion Between Quaternions and Other Representations

From Quaternion to Rotation Matrix

A unit quaternion $q = [w, x, y, z]$ can be converted to a 3x3 rotation matrix $R$ using the following formula:

R = [\begin{matrix} 1 - 2 (y^{2} + z^{2}) & 2 (x y - w z) & 2 (x z + w y) \\ 2 (x y + w z) & 1 - 2 (x^{2} + z^{2}) & 2 (y z - w x) \\ 2 (x z - w y) & 2 (y z + w x) & 1 - 2 (x^{2} + y^{2}) \end{matrix}]

Advantages of Quaternions

No Gimbal Lock: This is the most significant advantage. Quaternions provide a continuous and singularity-free representation of all 3D orientations.
Computationally EfficientComposing two rotations (multiplying two quaternions) is computationally faster than multiplying two 3x3 matrices. They also use less memory (4 vs. 9).
Smooth Interpolation (SLERP):Quaternions allow for a constant-speed interpolation between two orientations called Spherical Linear Interpolation (SLERP). This is crucial for generating smooth trajectories for robot arms or cameras. Euler angle interpolation, in contrast, is jerky and the speed of rotation is not constant.

Disadvantages of Quaternions

Not Intuitive: Their biggest drawback is that these deepshits are very difficult for humans to visualize. It's hard to look at the four numbers of a quaternion and immediately understand the orientation it represents, unlike the simple roll, pitch, yaw of Euler angles. But who cares when the machine can understand it better? insert AI joke