K-Means

K-means

K-means in a nutshell:
assign points $\to$ refit the cluster centres.

Both can come from optimizing a single objective function:

J = \sum_{i = 1}^{n} \sum_{k = 1}^{K} ε_{i k} ∥ x_{i} - μ_{k} ∥^{2}

Binary indicator:

ε_{i k} = {\begin{cases} 1 & if x_{i} \to k \\ 0 & otherwise \end{cases}

Basically $ε_{i k} = 1$ if $k = \arg min_{j} ∥ x_{i} - μ_{j} ∥^{2}$ and $ε_{i j} = 0$ for $j \neq k$ .

Finding $ε_{i k}$ , minimizing $J$ is easy.

ε_{i k} = {\begin{cases} 1 & if k = \arg min_{j} ∥ x_{i} - μ_{j} ∥^{2} \\ 0 & otherwise \end{cases}

Of course, the next step is to update $μ_{k}$ . We can think intuitively that the best place for $u_{k}$ would be in the middle of all that is in " $k$ ".

Enough of intuition lad, Here's your mathematical jargon:

For the fixed $k$ :

J_{k} = \sum_{i = 1}^{n} ε_{i k} ∥ x_{i} - μ_{k} ∥^{2}

\frac{\partial J_{k}}{\partial μ_{k}} = \sum_{i = 1}^{n} ε_{i k} (x_{i} - μ_{k}) = 0

Literally just the mean of all the points belonging to cluster $k$ , which is also refitting.

∴ μ_{k} = \frac{\sum_{i = 1}^{n} ε_{i k} x_{i}}{\sum_{i = 1}^{n} ε_{i k}}

Q&A

Q: Why initialize centres first?

A: If not done otherwise, i.e., using random centers to all points, makes it so that no points at all. $μ_{i} = 0$ , making it a dead centre.
On an unlucky assignment of centre this can happen too but very rarely either ways we will have closest cluster to any data point while the assignment step and algorithm keeps going.

E-step $\to$ Expectation step (Assignment step)
M-step $\to$ Maximization step (Refitting)

Error = {\begin{cases} 1 & if new min (∥ x_{n} - μ_{i} ∥^{2}) \\ 0 & otherwise \end{cases}

But this E-M step lead to local minima. We do random start on $K$ and then find which led to the lowest cost. So $K + +$ .

K++

Pick first centre randomly.

Then we have $D (x, c_{1})$ distance to Nearest centre, choose next centre by point $x_{n}$ with probability $D (x_{n})^{2}$ .
What this essentially does is that it favours points which are far away from already chosen centres making it more likely to pick a centre in a new cluster.

Use Cases

Lossy Compression

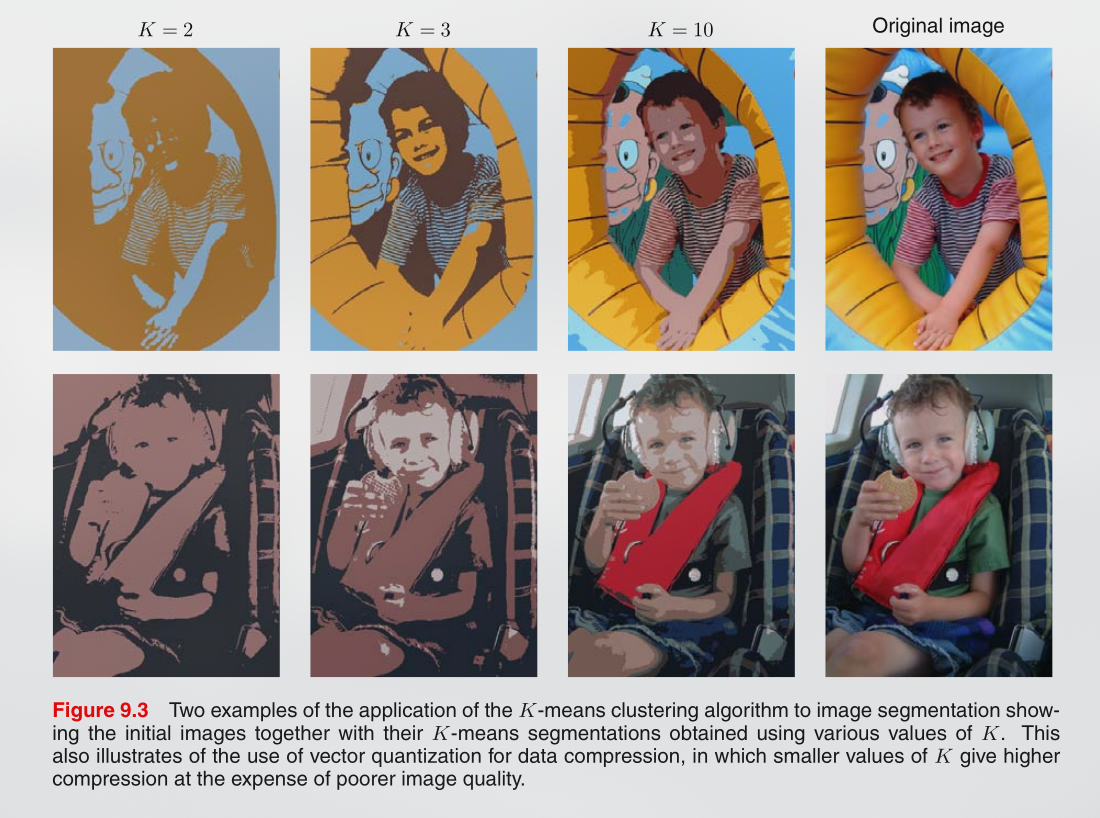
Pasted image 20250922160036.png

Image taken from Pattern Recognition and Machine Learning

We apply K-means in the following manner:
For each N data points, we only story the identity of k of the cluster to which it is assigned.
You also store the value of the K cluster-centres $u_{k}$ .

It's called a vector quantization framework.
$u_{k} \to$ code-book vectors

Example for Image segmentation:
For an image $(k, k_{bit})$ with $t$ bit precision, $N \times t$ bits is needed.

Figure:
So in our case of {R,G,B} with 8 bit precision we would need $24 N$ bits.
Now suppose we ﬁrst run K-means on the image data, and then instead of transmitting the original pixel intensity vectors we transmit the identity of the nearest vector $u_{k}$ . Because there are K such vectors, this requires $l o g_{2} (k)$ bits per pixel. We must also transmit the K code book vectors $u_{k}$ , which requires $24 K$ bits, and so the total number of bits required to transmit the image is $24 K + N l o g_{2} (k)$ (rounding up to the nearest integer).

Medoid

Medoid: (not mean, an actual point in the dataset)

min_{c \in S} \sum_{x \in S} D (x, c)

when $i, j \in S$ .

Limitations

Assumes spherical clusters
Hard assignments
Sensitive to outliers

To kind of tackle this we use Mixture Models.