Lorentz Transformation Equations

Good Resource:

• https://www.feynmanlectures.caltech.edu/II_26.html
• https://www.desmos.com/calculator/j4b0gp6vhw

For a frame moving with velocity $v$ along the $x$-axis, the Lorentz transformation equations are:

• Time Transformation:$$t^{\prime }=\gamma (t-\frac{vx}{c^2})$$
• Space Transformation:$$x^{\prime }=\gamma (x-vt)$$

Where $\gamma$ is the Lorentz factor(always greater than 1 btw):

Intuition Behind Lorentz Transformation

The Lorentz transformation ensures that the speed of light is constant ($c$) in all inertial reference frames. It modifies the time and space coordinates so that observers in different reference frames (moving relative to each other) will still measure the same speed for light.

• For example, consider a light beam emitted from the origin at $t=0$. In the stationary frame, the light moves according to $x=ct$. After applying the Lorentz transformation, the same light beam in a moving frame satisfies $x^{\prime }=c{t}^{\prime }$. This shows that light travels at speed $c$ in all frames, regardless of the observer's velocity.
• For me this understanding comes from a matrix transformation where speed of light is a eigenvector and we are shifting the space time according to that vector.

Space-Time Diagram for Lorentz Transformation

The following diagram shows the relationship between time ($t$) and space ($x$) in both the stationary frame $(t,x)$ and the moving frame $(t^{\prime },x^{\prime })$.

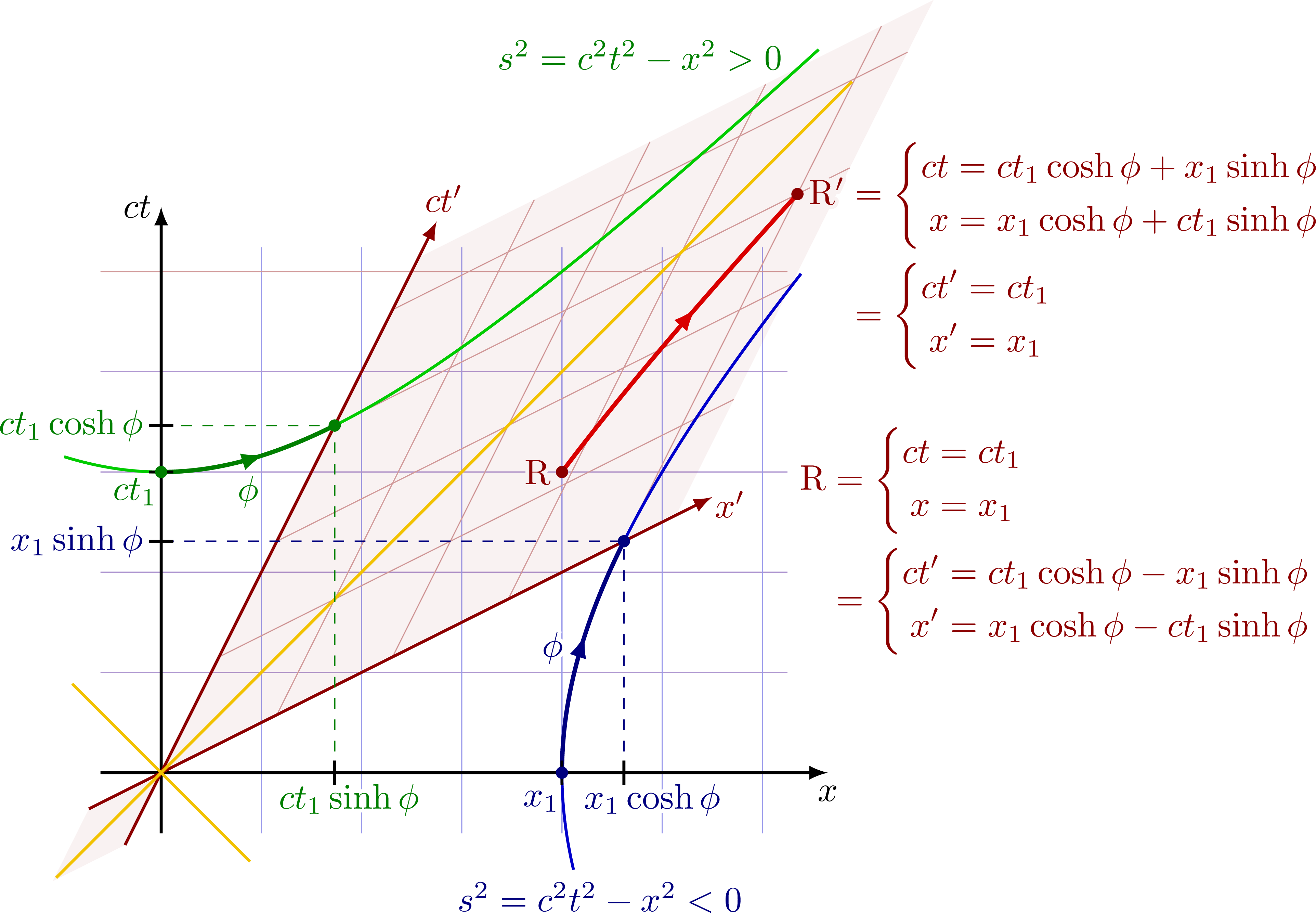
Visualizing Time Dilation with Lorentz Transformation

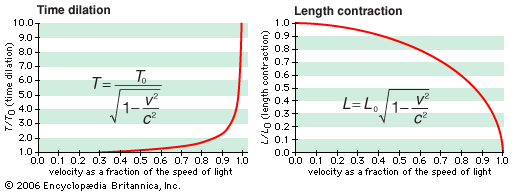
Time Dilation occurs because time passes differently for observers moving relative to each other. For an observer in motion, clocks in the stationary frame appear to run slower.

Intuition:

Imagine a moving object, say a spaceship, equipped with a clock. From the perspective of someone on Earth (stationary frame), the clock aboard the spaceship ticks more slowly. The Lorentz transformation shows that the time experienced by the moving spaceship ($t^{\prime }$) is less than the time experienced by the stationary observer ($t$), by a factor of $\gamma$.

To visualize this:

1. In the stationary frame, time passes normally along the $t$-axis.
2. In the moving frame, time is tilted along the $t^{\prime }$-axis. As a result, for the same amount of movement in space, less time elapses on the moving clock. This is time dilation.

Visualizing Length Contraction with Lorentz Transformation

Length Contraction is the phenomenon where an object moving relative to an observer appears shortened along the direction of motion. In the Lorentz transformation, this contraction happens because space is "squeezed" in the direction of motion.

Intuition:

If a spaceship is moving close to the speed of light, its length (in the direction of motion) appears contracted to an observer on Earth. The faster the spaceship moves, the more it contracts.

To visualize this:

1. In the stationary frame, the spaceship has a proper length $L$.
2. In the moving frame, this length is contracted by a factor of $\gamma$, and the new length $L^{\prime }=\frac{L}{\gamma }$ appears shorter.

Graph of Length Contraction and Time Dilation: