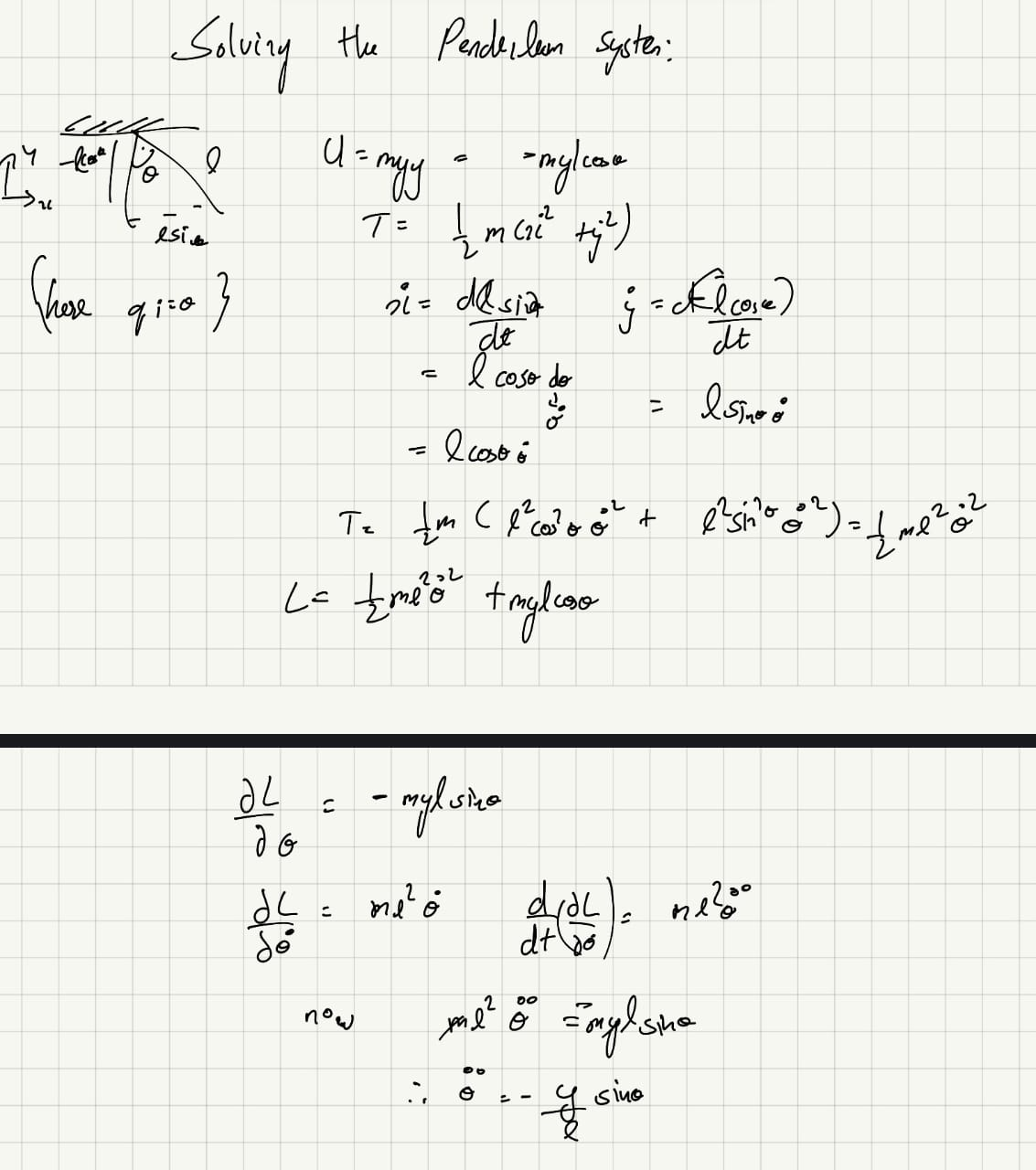Euler-Lagrange Equation

Good video to get intuition :

The Euler-Lagrange equation is a fundamental result of the calculus of variations and is derived from Hamilton’s principle of stationary action. It provides the equations of motion for a physical system once the Lagrangian is known.

Euler-Lagrange Equation:

For each generalized coordinate $q_{i}$ , the Euler-Lagrange equation is:

\frac{d}{d t} (\frac{\partial L}{\partial {\dot{q}}_{i}}) - \frac{\partial L}{\partial q_{i}} = 0

Intuition:

Soo what I have come to realize is the way this equation works is magical, that somehow it follows the rules stated before and finds the path that does the least action which we already know from Hamiltonian Principle, also this video explains the math behind it, but I didn't really get it, maybe someday I will re-visit this and get it, here's the video I am talking about .

But yeah it makes sense why all of these work in the first place after understanding that essentially what we are gonna solve for is the path with least action and that is what happens in reality.

Derivation:

Starting from Hamilton’s principle, $δ S = 0$ , we have the action:

S = \int_{t_{1}}^{t_{2}} L (q_{i}, {\dot{q}}_{i}, t) d t

Taking the variation of $S$ , we vary the path slightly and compute how the action changes. Setting the variation to zero yields the Euler-Lagrange equations, which are the equations of motion.

Example:

For a simple harmonic oscillator, the Lagrangian is:

L = \frac{1}{2} m {\dot{x}}^{2} - \frac{1}{2} k x^{2}

Applying the Euler-Lagrange equation:

\frac{d}{d t} (\frac{\partial L}{\partial \dot{x}}) - \frac{\partial L}{\partial x} = 0

yields the equation of motion:

m \ddot{x} + k x = 0

Pendulum exampolo

Pasted image 20241014200827.png